Разумеется, многие из нас могут вспомнить курсы геометрии из школьных дней. Эти прошлые занятия, проведенные на скамье, когда мы уставились на доску, на которой были изображены различные фигуры, покрытые закоулками, теорминами и другими загадочными символами, казались тяжелыми и сложными. Но сейчас время потекло непрерывной рекой, и мы оказываемся вновь перед этими фигурами, но с другой, более практической, точки зрения.
Каждая фигура имеет свою специфическую геометрическую форму. Одной из этих форм является треугольная призма, состоящая из трех равносторонних треугольников в основании и трех прямоугольных граней, соединяющих эти треугольники. Важно отметить, что эта форма часто встречается в реальном мире, например, в архитектуре и строительстве. Понимание и умение расчета периметра такой фигуры может пригодиться в различных ситуациях, связанных с этой областью деятельности.
Сегодня мы изучим, как найти периметр треугольной призмы. Итак, если вы когда-либо задумывались о том, как определить длину всех граней этой фигуры, то вы попали по адресу! Наша статья предлагает простую инструкцию, которая поможет вам разобраться с этой задачей и применить ее на практике. Следуйте инструкциям и вы сможете легко определить периметр треугольной призмы, необходимый для решения различных геометрических задач и проблем в повседневной жизни.
Уникальный раздел статьи: Как определить общую длину всех сторон в правильной геометрической фигуре-призме
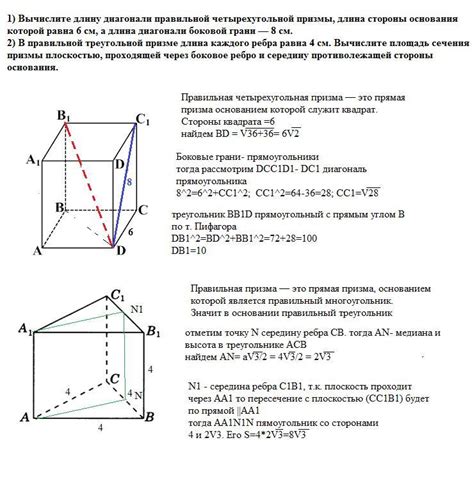
В этом разделе мы рассмотрим простую и эффективную методику определения суммы длин всех сторон в особой трехмерной структуре, у которой каждая грань представляет собой равносторонний треугольник.
Для начала, нам понадобится разложить трехмерную фигуру-призму на двумерную плоскость, чтобы лучше визуализировать и проанализировать ее структуру. Создав таблицу с данными о каждой грани призмы, мы сможем проанализировать их длины и соответствующим образом их суммировать.
| Грань | Длина стороны 1 | Длина стороны 2 | Длина стороны 3 |
|---|---|---|---|
| Грань 1 | a | b | c |
| Грань 2 | a | b | c |
| Грань 3 | a | b | c |
| Грань 4 | a | b | c |
| Грань 5 | a | b | c |
| Грань 6 | a | b | c |
Здесь a, b и c представляют длины каждой стороны равностороннего треугольника. После заполнения таблицы, произведем простые математические вычисления: сложим длины всех сторон для каждой грани и просуммируем полученные значения. Полученная сумма будет представлять общую длину всех сторон в правильной треугольной призме.
Таким образом, используя данную простую инструкцию и таблицу, вы легко сможете определить общую длину всех сторон в правильной треугольной призме. Следуйте нашему руководству и получите точный результат без лишней сложности и трудностей.
Описание правильной треугольной призмы и ее внешний вид
В этом разделе мы рассмотрим особенности правильной треугольной призмы и представим ее внешний вид. Эта геометрическая фигура обладает определенными свойствами, которые делают ее уникальной и интересной.
Правильная треугольная призма состоит из трех треугольных граней и трех прямоугольных граней. Треугольные грани образуют основание призмы, которые представляют собой равносторонний треугольник. Прямоугольные грани соединяют основание призмы и образуют боковые стороны. В результате получается трехмерная фигура с плоскими гранями.
Важно отметить, что все стороны и углы в правильной треугольной призме равны между собой. Это делает ее симметричной и одинаковой по форме. Благодаря этим особенностям, правильная треугольная призма обладает уникальным и эстетическим внешним видом.
Основываясь на описанных характеристиках, мы можем представить правильную треугольную призму как геометрическую фигуру, которая имеет равносторонний треугольник в качестве основания и прямоугольные грани, соединяющие это основание. Ее симметричная форма и эстетически приятный внешний вид делают ее интересной и привлекательной для изучения.
Как определить общую длину периферии основания регулярной треугольной призмы

В данном разделе мы рассмотрим способы вычисления суммарной длины всех сторон основания треугольной призмы, конструктивно представляющей собой трехмерную фигуру с правильным треугольным основанием.
Для расчета периметра основания треугольной призмы необходимо учесть, что оно характеризуется равными сторонами и углами в каждой вершине. Величина периметра является суммой длин всех сторон, ограничивающих основание.
Для нахождения периметра можно воспользоваться математической формулой, исходя из длины одной стороны основания треугольника. Умножив ее на количество сторон основания и суммируя полученные значения, мы можем получить общую длину периферии.
Как определить высоту правильной треугольной призмы
В этом разделе мы рассмотрим методы и подходы для определения высоты правильной треугольной призмы. Знание высоты играет важную роль при решении задач, связанных с треугольной призмой, так как она позволяет определить объем, площадь поверхности и другие характеристики этой геометрической фигуры.
Для начала, давайте вспомним основные понятия и свойства треугольной призмы. Высота - это перпендикуляр, опущенный из вершины треугольника к основанию, образуя прямой угол. Важно отметить, что призма будет считаться правильной, если ее боковые грани являются равнобедренными треугольниками.
Существует несколько подходов к определению высоты правильной треугольной призмы. Один из них основан на использовании теоремы Пифагора, которая позволяет найти длину высоты треугольника по длинам его сторон. Еще один метод предлагает использовать геометрические соображения и свойства подобных треугольников.
- Метод 1: используя теорему Пифагора
- Метод 2: применение геометрических свойств
Выбор метода зависит от доступных данных и предпочтений решателя задачи.
В следующих разделах мы подробнее рассмотрим каждый из этих методов и предоставим инструкции, которые помогут вам определить высоту правильной треугольной призмы в конкретных случаях.
Как применять формулу для вычисления окружности структуры призмы
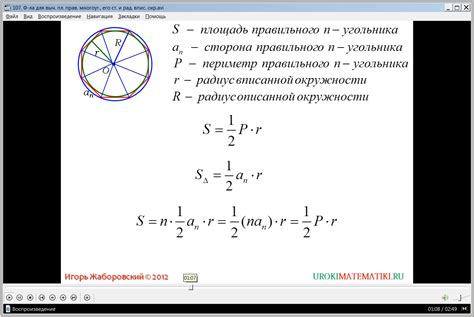
В этом разделе мы рассмотрим способ применения формулы, которая позволяет определить периметр треугольного основания призмы. При помощи данной формулы вы сможете легко и точно рассчитать периметр структуры, не зависимо от ее размера или формы.
Step 1: Вначале важно определить тип треугольника, который является основанием вашей призмы. Например, это может быть равнобедренный, прямоугольный или разносторонний треугольник. Зная тип треугольника, вы будете знать, какую формулу использовать для расчета его периметра.
Step 2: После определения типа треугольника, используйте соответствующую формулу для вычисления периметра его сторон. Например, для равнобедренного треугольника формула будет выглядеть следующим образом: периметр = 2 * a + b, где a - длина равных сторон, а b - длина основания треугольника.
Step 3: Зная периметр основания треугольника, вы можете применить дополнительную формулу для расчета периметра всей призмы. Эта формула состоит из умножения периметра основания на высоту призмы.
Обратите внимание: это только пример использования формулы для расчета периметра призмы. В зависимости от особенностей вашей призмы, формула может изменяться. Всегда следуйте конкретным инструкциям или обращайтесь к профессионалам, если вам требуется более точный и подробный расчет периметра вашей призмы.
Пример вычисления окружности правильной треугольной принадлежности

Данный раздел предоставляет пример расчета окружности для объекта, который имеет геометрическую форму правильного треугольника и призму. Обратные круги устарели, дамы и госпада! Давайте узнаем, как посчитать периметр для этой уникальной фигуры.
Шаг 1: Убедитесь, что вы имеете правильную треугольную призму перед собой. Она должна состоять из трех правильных треугольных граней и трех прямоугольных граней.
Шаг 2: Определите длину стороны треугольника. Это расстояние, измеряемое от одной вершины треугольника до противоположной стороны.
Шаг 3: Умножьте длину стороны треугольника на 3. Так как у нас правильная треугольная призма, каждая сторона треугольника будет иметь одинаковую длину. Полученное значение будет являться периметром одной грани.
Шаг 4: Умножьте периметр одной грани на 3, чтобы найти общий периметр правильной треугольной призмы. Так как у нас три грани, каждая с одинаковым периметром, результат будет представлять собой полную окружность фигуры.
Запомните, что правильная треугольная призма имеет все стороны одинаковой длины, и каждая сторона состоит из трех сегментов равной длины.
Применение знания о периметре призмы в практике
Знание о периметре призмы может быть полезно и находить применение в различных жизненных ситуациях. Определение периметра призмы, то есть суммы длин всех ее сторон, позволяет решать задачи, связанные с измерением и расчетами.
Например, при строительстве дома или создании архитектурного проекта, знание о периметре призмы поможет определить длину материала, необходимого для покрытия стен или создания ограждения. Также, при проектировании мебели, знание о периметре призмы позволит учесть все необходимые мерки и определить требуемое количество используемых материалов.
Понимание периметра призмы также полезно при работе с картографическими данными. Зная периметр земельного участка или территории, можно определить необходимое количество заборного материала или длину провода для установки ограждения. Кроме того, знание о периметре призмы может быть полезным при проведении инженерных изысканий для создания дорожной сети или инфраструктуры, такой как водоснабжение или электрические сети.
| Практическое применение знания о периметре призмы: | - Расчет необходимого количества материала при строительстве или проектировании мебели |
| - Определение длины забора или провода для ограждения территории | |
| - Проведение инженерных изысканий для создания дорожной сети и инфраструктуры |
Вопрос-ответ

Как найти периметр правильной треугольной призмы?
Для того чтобы найти периметр правильной треугольной призмы, сначала необходимо измерить длину стороны основания треугольника. Затем умножьте эту длину на 3, так как у правильной треугольной призмы все стороны основания равны. Наконец, добавьте к полученному результату периметр боковых граней, который равен 3 разам длины одной стороны основания.
Что такое правильная треугольная призма?
Правильная треугольная призма - это трехмерная геометрическая фигура, у которой основание представляет собой равносторонний треугольник, а все боковые грани являются равновеликими и равнобедренными треугольниками. Такая призма имеет оси симметрии, проходящие через вершину основания и середины противоположных сторон основания.
Чем полезна периметр правильной треугольной призмы?
Периметр правильной треугольной призмы является важной характеристикой этой фигуры, так как он позволяет определить длину окружности, охватывающей основание и боковые грани призмы. Зная периметр, можно также вычислить площадь поверхности и объем призмы. Периметр также может быть использован для построения трехмерной модели призмы или для вычисления других характеристик фигуры.
Как измерить длину стороны основания треугольной призмы?
Для измерения длины стороны основания треугольной призмы, используйте линейку или сантиметровую ленту. Положите линейку или сантиметровую ленту вдоль одной стороны основания и измерьте расстояние от начала до конца этой стороны. Полученная величина и будет длиной стороны основания треугольной призмы.
Какой уникальной особенностью обладает правильная треугольная призма?
Одной из уникальных особенностей правильной треугольной призмы является равенство всех углов между боковыми гранями, которые составляют по 60 градусов. Это делает призму симметричной и гармоничной внешне. Также в правильной треугольной призме все стороны основания и боковые грани равны между собой. Это приводит к тому, что призма обладает определенными соотношениями между своими характеристиками, что делает ее уникальной.



