Когда мы сталкиваемся с геометрическими задачами, особенно связанными с расчетами площадей, на первый взгляд может показаться, что решение является сложным и запутанным. Однако, каждая задача имеет свою логику и подход, который позволяет нам справиться с ней безболезненно и эффективно.
Сегодня мы рассмотрим одну из таких задач - определение площади ромба при известной длине одной его стороны и угле 60 градусов. Эта геометрическая фигура, обладающая четырьмя равными сторонами и двумя параллельными противоположными углами, может поначалу показаться сложной для изучения, но на самом деле алгоритм ее расчета довольно прост.
Для начала, давайте вспомним основные свойства ромба - это фигура, у которой все стороны равны между собой, и каждая из этих сторон образует угол в 45 градусов с горизонтальной осью. Также нам известно, что сумма углов в ромбе составляет 360 градусов.
Вычисление площади ромба при указанной длине стороны и угле 60 градусов
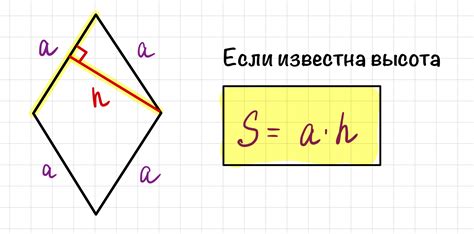
В данном разделе рассмотрим способ нахождения площади ромба, основываясь на известной длине стороны и угле между этой стороной и соседней стороной, равным 60 градусов.
Для начала определим, что ромб - это плоская геометрическая фигура, у которой все стороны имеют одинаковую длину, а соседние углы равны. Угол между сторонами можно найти, используя геометрические свойства ромба и зная его угол.
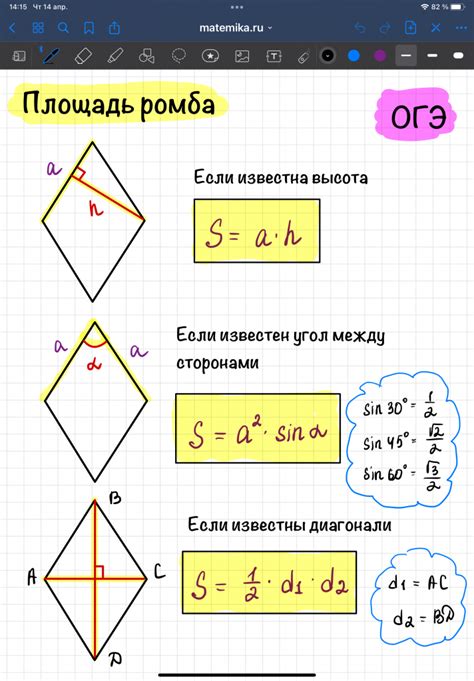
Для вычисления площади ромба, когда известны длина одной стороны и угол между этой стороной и соседней стороной, можно использовать следующую формулу:
- Найдите площадь треугольника, образованного двумя соседними сторонами ромба и отрезком, соединяющим их концы. Для этого используйте формулу площади треугольника s = (a * b * sin(α))/2, где a и b - длины сторон треугольника и α - угол между ними.
- Умножьте полученную площадь треугольника на 2, чтобы получить площадь ромба, так как ромб состоит из двух одинаковых треугольников.
Теперь, когда мы знаем алгоритм вычисления площади ромба при известной длине стороны и угле 60 градусов, можно приступить к конкретным примерам и практическим вычислениям. Каждый ромб в зависимости от заданных параметров будет иметь свою уникальную площадь, которую можно найти с помощью указанных шагов.
Глубже изучаем основные признаки ромбов
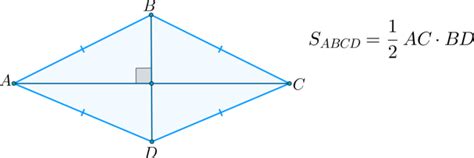
В этом разделе мы погружаемся в изучение основных характеристик ромбов, фигур с уникальными свойствами и геометрической структурой. Раскроем необычность и красоту этой формы, не упуская из виду ее важные особенности и применения в различных сферах.
1. Геометрическая структура ромбов:
- Вершины и ребра
- Диагонали и их свойства
- Углы и их особенности
2. Симметрия и оси симметрии ромбов:
- Осевая симметрия
- Центральная симметрия
- Переносимая симметрия
3. Формулы и свойства ромбов:
- Площадь ромба
- Периметр ромба
- Формулы для вычисления сторон и углов ромба
4. Применение ромбов в реальной жизни:
- Архитектура и декоративное искусство
- Математика и геометрия
- Электротехника и электроника
Исследуя эти основные свойства и применения ромбов, мы погружаемся в особый мир геометрии, расширяем свои знания и умение решать разнообразные задачи, а также обнаруживаем красоту и гармонию в окружающем нас мире.
Метод 1: Определение длины диагоналей ромба
Для начала нам понадобятся значения стороны и угла ромба. Назовем сторону ромба "a", а угол между диагоналями "α". Также мы будет использовать некоторые тригонометрические свойства для нахождения значений диагоналей.
| Величина | Обозначение |
|---|---|
| Сторона ромба | a |
| Угол между диагоналями | α |
| Длина первой диагонали | d1 |
| Длина второй диагонали | d2 |
Мы можем использовать формулы из геометрии и тригонометрии для нахождения диагоналей ромба на основе заданных значений стороны и угла. При этом тригонометрические функции, такие как синус и косинус, позволяют нам связать угол α с длинами диагоналей.
Применяя эти формулы, мы можем определить значения длины первой и второй диагоналей ромба. Зная эти значения, мы сможем вычислить площадь ромба по формуле, использующей длины диагоналей.
Метод 2: Определение площади ромба с помощью математической формулы
В данном разделе мы рассмотрим альтернативный способ вычисления площади ромба при известной длине стороны и значении угла 60 градусов. Для этого мы воспользуемся математической формулой, которая позволяет нам точно определить площадь ромба без необходимости знать все его стороны.
Прежде чем перейти к формуле, важно понимать некоторые особенности ромба. Ромб - это четырехугольник с четырьмя равными сторонами. Также, угол между двумя соседними сторонами ромба всегда равен 60 градусам. Эти характеристики и помогут нам определить его площадь.
| Дано | Формула |
|---|---|
| Длина стороны ромба (a) | Площадь = (a * a * sin(60 градусов)) |
В формуле выше мы используем значения длины стороны ромба (a) и синуса угла 60 градусов, который равен √3/2. Подставив эти значения в формулу, мы сможем вычислить площадь ромба.
Например, если сторона ромба равна 6 единицам длины, то пользуясь формулой, мы найдем площадь ромба как (6 * 6 * √3/2), что равно 18√3 квадратных единиц.
Теперь, имея математическую формулу для определения площади ромба, вы сможете быстро и точно найти его площадь при заданной длине стороны и значении угла 60 градусов.
Практическое применение рассчета площади ромба
Например, при проектировании зданий и сооружений инженерам необходимо знать площадь поверхности, которую займет ромбовидный элемент, чтобы точно рассчитать объем материала для его изготовления. Это позволяет избежать излишних расходов или недостаточности материалов, что важно с точки зрения экономической эффективности и надежности конструкции.
Еще одним примером применения расчета площади ромба является сфера дизайна. Дизайнеры и архитекторы используют ромбовидные формы в интерьере и экстерьере, чтобы создать визуальные эффекты, подчеркнуть особенности пространства или добавить оригинальность в дизайне. При этом знание площади ромба позволяет оптимально размещать эти формы и добиваться желаемого эстетического результата.
Расчет площади ромба также находит применение в строительстве, особенно в геометрии при устройстве перекрытий или крыш. Знание площади ромба помогает точно определить объем материалов и размеры, что в свою очередь обеспечивает прочность и безопасность конструкции.
Осознание практического применения рассчета площади ромба является важным аспектом овладения математическими навыками. Это демонстрирует, что математика является языком, который может быть использован в различных областях нашей жизни, и абстрактные концепции могут быть применены для конкретных задач и решений.
Вопрос-ответ

Как найти площадь ромба, если известна длина одной его стороны и значение угла между этой стороной и соседней?
Для вычисления площади ромба при заданной стороне и угле между этой стороной и соседней мы можем воспользоваться следующей формулой: S = a^2 * sin(α), где S - площадь ромба, a - длина одной стороны ромба, α - значение угла между этой стороной и соседней. В данном случае, если нам дана длина стороны ромба и значение угла 60 градусов, мы можем подставить значения в формулу и получить результат.
Как вычислить площадь ромба, если известно, что одна из его сторон равна 8 см, а угол между этой стороной и соседней составляет 60 градусов?
Для вычисления площади ромба при заданной стороне и угле между этой стороной и соседней мы можем воспользоваться формулой S = a^2 * sin(α), где S - площадь ромба, a - длина одной стороны ромба, α - значение угла между этой стороной и соседней. Подставляя в данную формулу значения из условия (a = 8 см, α = 60 градусов), мы получаем S = 8^2 * sin(60°) = 64 * √3/2 = 32√3 см^2. Таким образом, площадь ромба составляет 32√3 квадратных сантиметра.
Можно ли найти площадь ромба, если известна только длина одной из его сторон?
Да, можно найти площадь ромба, если известна длина одной из его сторон. Для этого необходимо знать также значение угла между этой стороной и соседней. С помощью геометрических формул и свойств ромба можно вычислить площадь, исходя из этих данных.
Какие формулы нужно использовать для нахождения площади ромба при заданной стороне и угле?
Для вычисления площади ромба при заданной стороне и угле между этой стороной и соседней используется формула S = a^2 * sin(α), где S - площадь ромба, a - длина одной стороны ромба, α - значение угла между этой стороной и соседней.
Как найти площадь ромба, если известна длина одной его стороны и угол между этой стороной и более длинной диагональю?
Для нахождения площади ромба при известной стороне и угле 60 градусов, нужно использовать следующую формулу: S = a² * sin(60), где а - длина стороны ромба. В данном случае, площадь равна квадрату длины стороны, умноженному на половину квадратного корня из 3.
Как вычислить площадь ромба, если известны длины его стороны и одной его диагонали, а также угол, образованный этой стороной и диагональю?
Площадь ромба при заданной стороне и угле 60 градусов можно найти, используя формулу: S = a * d * sin(60), где а - длина стороны, d - длина диагонали. В данном случае, площадь равна произведению длин стороны и диагонали, умноженному на половину квадратного корня из 3.



